Your server has received a package of N incoming requests. Handling the K-th request (for K from 0 to N − 1) will take A[K] seconds.

The load balancer has to drop two acquired requests and distribute the rest of them between three workers in such a way that each worker receives a contiguous fragment of requests to handle, and finishes handling them in exactly the same moment as the other workers. No two workers should receive the same request to compute.

The load balancer's distribution of requests is performed by selecting two requests that will be dropped, and which will split the array into three contiguous parts that will be allocated to the workers. More precisely, if requests 2 and 5 are chosen by the load balancer from a package of 9 requests, then:

• the 0-th to 1-st requests will be handled by the first worker,
• the 3-rd to 4-th requests will be handled by the second worker,
• the 6-th to 8-th requests will be handled by the third worker.

Such a distribution will be correct if each worker receives requests equalling the same total amount of handling time.

Write a function solution that, given an array A of N integers representing the time of execution of consecutive tasks, returns true if it is possible for the load balancer to choose two requests that will determine an even distribution of requests among three workers, or false otherwise.

Examples:

1. Given A = [1, 3, 4, 2, 2, 2, 1, 1, 2], the function should return true, as choosing requests 2 and 5 results in a distribution giving 4 seconds of handling time to each worker, as explained in the following image:

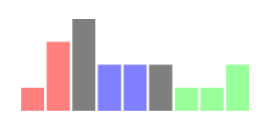
Given A = [1, 1, 1, 1, 1, 1], the function should return false.

Given A = [1, 2, 1, 2, ..., 1, 2] of length 20,000, the function should return true.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [5..100,000];
• each element of array A is an integer within the range [1..10,000].