No.1 在既定时间做作业的学生人数 ★ 解题思路

枚举一次每个学生的写作业时间, 判断这一段时间是否包含 queryTime 即可.

代码展示

class Solution {
   public int busyStudent(int[] startTime, int[] endTime, int queryTime) {
       int res = 0;
       for (int i = 0; i < startTime.length; i++) {
           res += (startTime[i] <= queryTime && queryTime <= endTime[i]) ? 1 : 0;
       }
       return res;
   }
}

No.2 重新排列句子中的单词 ★解题思路

拆分, 排序, 重组即可. 详见代码注释.

代码展示

class Solution {
   public String arrangeWords(String text) {
       // 将单词拆分出来
       String[] words = text.split(" ");
       // 首字母变成小写
       words[0] = words[0].toLowerCase();
       // 按照长度排序. sort 是稳定的排序, 所以可以保持长度相等的字符串的相对顺序
       Arrays.sort(words, Comparator.comparingInt(String::length));
       // 首字母变成大写
       words[0] = words[0].substring(0, 1).toUpperCase() + words[0].substring(1);
       // 将单词合并成一个字符串
       return String.join(" ", words);
   }
}

No.3 收藏清单

★解题思路

该题目数据范围较小, 最多只有 100 个收藏清单. 因此我们可以枚举判断每一个清单是否其他任一清单的子集.

至于如何判断一个 List 是否另一个 List 的子集, 有很多种方式:

1.使用 Set 的 containsAll() 方法

2.排序, 逐一判断

下面的代码使用的是第二种方式, 详细过程见代码注释.

代码展示

class Solution {
   public List<Integer> peopleIndexes(List<List<String>> favoriteCompanies) {
       // 将每个收藏清单排序, 便于判断
       for (var list : favoriteCompanies) {
           Collections.sort(list);
       }
       List<Integer> res = new ArrayList<>();        
       for (int i = 0; i < favoriteCompanies.size(); i++) {
           boolean flag = true;
           // 判断是否存在一个收藏清单包含当前的 i 号清单
           for (var list : favoriteCompanies) {
               if (isSubSet(favoriteCompanies.get(i), list)) {
                   flag = false;
                   break;
               }
           }
           if (flag) {
               res.add(i);
           }
       }
       return res;
   }

   private boolean isSubSet(List<String> sub, List<String> list) {
       // 判断 sub 是否 list 的子集, 并且这两个 List 都是有序的
       if (sub.size() >= list.size()) {
           return false;
       }
       int i = 0;
       // 总时间复杂度 o(n)
       // 逐个判断 sub 中的每个元素是否都存在于 list 中
       for (var s : sub) {
           while (i < list.size() && !list.get(i).equals(s)) {
               i++;
           }
           if (i == list.size()) {
               return false;
           }
       }
       return true;
   }
}

No.4 圆形靶内的最大飞镖数量

★解题思路

这个题目看似很难, 但是实际需要的几何知识并不多, 画出图来会容易理解很多.

在圈住的点最多的情况下, 必然可以使得至少两个点处于圆周上.

我们只需要枚举哪两个点在圆周上即可, 对于 pi 和 pj 在圆周上的情况, 圆心即可确定, 如图:

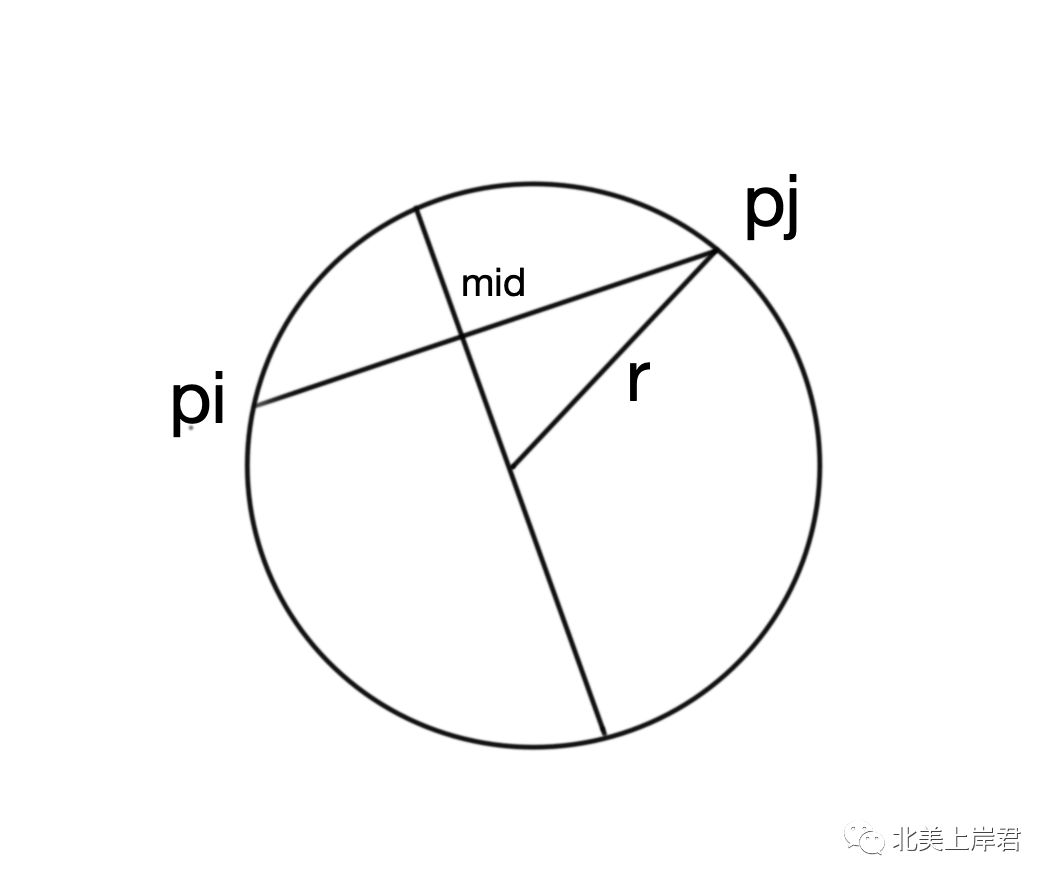
对称地, 圆心还有一种情况, 就是在上面. 即任意一对点都可以确定两个圆心. 我们枚举每一对点, 然后对于确定的圆心计算这个圆可以圈出多少个点, 最后取最大即可.

代码展示

class Solution {
   final double eps = 1e-8;

   public int numPoints(int[][] points, int r) {
       int n = points.length;
       int res = count(points, points[0][0], points[0][1], r);
       for (int i = 0; i < n; i++) {
           for (int j = i + 1; j < n; j++) {
               // 枚举两点 pi 和 pj, 假设它们在圆周上
               var pi = points[i];
               var pj = points[j];
               // i 和 j 的中点
               double midx = (pi[0] + pj[0]) / 2.0;
               double midy = (pi[1] + pj[1]) / 2.0;
               // i 和 j 的横纵坐标之差
               double dx = pi[0] - pj[0];
               double dy = pi[1] - pj[1];
               // i 和 j 的距离
               double dis = Math.sqrt(dx * dx + dy * dy);
               // 中点与圆心的距离 (勾股定理)
               double disR = Math.sqrt(r * r - dis * dis / 4);
               // 中点与圆心的横纵坐标之差的比例 (相似三角形)
               double dxR = -dy / dis;
               double dyR = dx / dis;
               // 圆心的两种情况
               double x = midx + dxR * disR;
               double y = midy + dyR * disR;
               res = Math.max(res, count(points, x, y, r));
               x = midx - dxR * disR;
               y = midy - dyR * disR;
               res = Math.max(res, count(points, x, y, r));
           }
       }
       return res;
   }

   public int count(int[][] points, double x, double y, int r) {
       int ans = 0;
       for (var p : points) {
           double dx = x - p[0];
           double dy = y - p[1];
           if (dx * dx + dy * dy <= r * r + eps) {
               ans++;
           }
       }
       return ans;
   }
}

杭州上岸算法网络科技有限公司

上岸科技是一家【死磕100%上岸率】的小公司。

核心团队和老师均来自于行业内知名公司，我们坚持采用小班课形式，并结合大量”面试式“和”白板“的教学和交流形式，最终做到摆渡【每个人】成功上岸的承诺。

我们对每个人负责，上岸，一个都不能少！